Recently, I saw a reference to
an interesting piece from 2013 by
Peter Grogono, a computer scientist now retired from Concordia University. It's to do with checking the "quality" of a (pseudo-) random number generator.
Specifically, Peter discusses what he calls "The Pickover Test". This refers to the following suggestion that he attributes to Clifford Pickover (1995, Chap. 31):
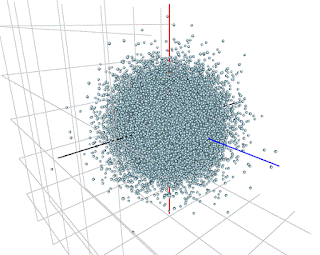
"Pickover describes a simple but quite effective technique for testing RNGs visually. The idea is to generate random numbers in groups of three, and to use each group to plot a point in spherical coordinates. If the RNG is good, the points will form a solid sphere. If not, patterns will appear.
When it is used with good RNGs, the results of the Pickover Test are rather boring: it just draws spheres. The test is much more effective when it is used with a bad RNG, because it produces pretty pictures."
Peter provides some nice examples of such pretty pictures!
I thought that it would be interesting to apply the Pickover Test to random numbers produced by the (default) RNG's for various distributions in R.
Before looking at the results, note that is the support of the distribution in question is finite (e.g., the Beta distribution), then the "solid sphere" that is referred to in the Pickover Test will become a "solid box". Similarly, if the support of the distribution is the real half-line (e.g., the Chi-Square distribution), the "solid sphere" will become a "solid quarter-sphere".
You can find the R code that I used on the
code page that goes with this blog. Specifically, I used the "rgl" package for the 3-D plots.
Here are some of my results, in each based on a sequence of 33,000 "triplets" of random numbers:
(i) Standard Normal (using "rnorm")
(ii) Uniform on [0 , 1] (using "runif")
(iii) Binomial [n = 100, p = 0.5] (using "rbinom")
(iv) Poisson [mean = 10] (using "rpois")
(v) Standard Logistic (using "rlogis")
(vi) Beta [1 , 2] (using "rbeta")
(vii) Chi-Square [df = 5] (using "rchisq")
(vii) Student-t [df = 3] (using "rt")
(viii) Student-t [df = 7] (using "rt")
(Note that if you run my R code you can rotate the resulting 3-D plots to change the viewing aspect by holding the left mouse key and moving the mouse. You can zoom in and out by "scrolling".)
On the whole, the results look pretty encouraging, as you'd hope! One possible exception is the case of the Student-t distribution with relatively small degrees of freedom.
Of course, the Pickover "Test" is nothing more than a quick visual aid that can alert you to possible problems with your RNG. It's not intended to be a substitute for more formal, and more specific, hypothesis tests for the distribution membership, independence, etc., of your random numbers..
References
Adler, D., D. Murdoch, et al., 2017' 'rgl' package, version 0-98.1.
Pickover, C., 1995.
Keys to Infinity. Wiley, New York.
© 2017, David E. Giles